IT Tutorial IT Tutorial | Oracle DBA | SQL Server, Goldengate, Exadata, Big Data, Data ScienceTutorial
Merhaba,
Secret Sharing yöntemi ilk defa 1979 yılında Shamir ve Blakley tarafından ortaya atılmıştır. Bu yönteme aynı zamanda ( k,n ) eşik şeması da denmektedir. Secret Sharing metodu Ses ve Text veriler üzerinde de uygulanabildiği gibi görüntü üzerinde de uygulanabiliyor Bu yöntemin ana fikri orijinal bir resmi n tane parçaya ayırmak ardından da bunu n tane insana paylaştırmaktır. En az k tane resim bir araya geldiğindeyse orijinal görüntü elde edilmesi şeklindedir. Thien ve Lin adı verilen 2 tane araştırmacı Shamir’in yöntemini kullanarak oluşturdukları Gizlilik paylaşımı şemasını aşağıda ele alınmıştır.
Thien Ve Lin Gizlilik Paylaşım Şeması
Thien ve Lin adlı 2 araştırmacı Shamir in ortaya attığı Gizlilik paylaşımı şemasını kullanarak ( k,n ) eşik tabanlı görüntü paylaşımını ortaya atmışlardır.
Bu yöntemin ana fikri |S| boyutundaki P adlı resimden n tane paylaştırılmış görüntü elde edebilmek için (k-1). Dereceden bir polinom elde etmektir. O polinomun matematiksel olarak ifade edilmiş şekli aşağıdadır.
Sx (i,j) =( P ( ik+1, j) + P( ik+2, j)x +P( ik+3,j)x2 +……+P( ik+k,j)xk-1 ) ( mod p )
Bu yöntemde oluşturulacak olan Gizli görüntülerin boyları orijinal görüntünün 1/k sı büyüklükte olmalıdır. Görüntü n tane parçaya ayrıldıktan sonra en az k tanesi bir araya geldiğinde orijinal görüntü tekrar elde edilmelidir.
Görüntüler n parçaya ayrıldıktan sonra k tanesinin bir araya gelmesiyle orijinal görüntünün tekrar elde edilmesi için Lagrange interpolation yöntemi kullanılmaktadır. İşte yöntemin matematiksel ifadesi:
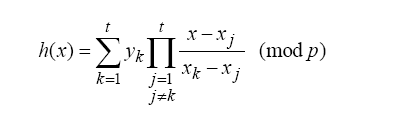
Örneğin elimizde şu polinom olsun:
Ve bu polinoma ait olan görüntüyü 6 parçaya ayırmış olalım.6 parça içerisinden 3 tane parçayı birleştirerek görüntüyü elde etmek istersek her bir nokta ve ona karşı düşen polinomda ki değeri şöyle olur.
Bu noktalar içerisinden herhangi 3 tane alındığında bu noktalar ve karşı düştüğü değerler aşağıdaki gibi olsun:
.
Bu 3 noktaya karşı düşen Lagrange interpolation değerleri şunlar olacaktır.
Şimdi bu 3 değerden hareket ederek ilk durum oluşturulabilir yani orijinal görüntüye karşı düşen değer ve bunu elde etmek için gerekli fonksiyon aşağıdaki gibi olur.
Bu toplam sembolünü matematiksel olarak açıldığında ve gerekli değerler yerine koyulduğunda şu polinom elde edilecektir.
Bu polinom düzenlendiğinde son sonuç önceki ilk polinom olacaktır ve buda işlemin doğru olduğuna dair bir ispat teşkil etmektedir.
Aşağıda ki örnekte görüntü 5 tane parçaya ayrılmış olup bunlardan en az 3 tanesi bir araya geldiğinde ise orijinal görüntünün elde edildiği gösterilmiştir.
Şekil-6 : Gri görüntü 6 parçaya ayrılmıştır.Herhangi 4 tanesi bir araya geldiğinde orijinal görüntü elde edilmektedir
