Hello, in this article, we continue the topic Unsupervised Learning.
Read the previous post before this post.
Dimension reduction
Dimension reduction finds patterns in data, and uses these patterns to re-express it in a compressed form. This makes subsequent computation with the data much more efficient and this can be a big deal in a world of big dataset.
Principal Component Analysis (PCA)
PCA performs dimension reduction in two steps, and the first one, called “de-correlation” , doesn’t change the dimension of the data at all.
Example
https://drive.google.com/file/d/1v6c5KhEXPvGinR0alinqYaqo-_of9agw/view?usp=sharing
You can access the entire linked code above.
import matplotlib.pyplot as plt
from scipy.stats import pearsonr
width = grains[:,0]
# Assign the 1st column of grains: length
length = grains[:,1]
# Scatter plot width vs length
plt.scatter(width,length)
plt.axis('equal')
plt.show()
# Calculate the Pearson correlation
correlation, pvalue = pearsonr(width,length)
# Display the correlation
print(correlation)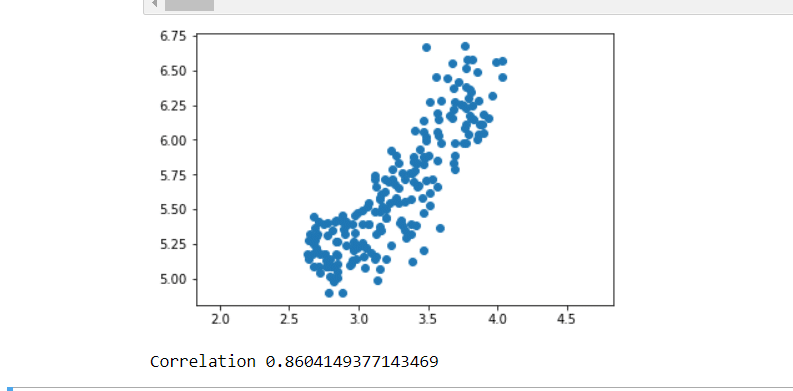
from sklearn.decomposition import PCA
# Create PCA instance: model
model = PCA()
# Apply the fit_transform method of model to grains: pca_features
pca_features = model.fit_transform(grains)
# Assign 0th column of pca_features: xs
xs = pca_features[:,0]
# Assign 1st column of pca_features: ys
ys = pca_features[:,1]
# Scatter plot xs vs ys
plt.scatter(xs, ys)
plt.axis('equal')
plt.show()
# Calculate the Pearson correlation of xs and ys
correlation, pvalue = pearsonr(xs, ys)
# Display the correlation
print(correlation)
See you in the next article
 IT Tutorial IT Tutorial | Oracle DBA | SQL Server, Goldengate, Exadata, Big Data, Data ScienceTutorial
IT Tutorial IT Tutorial | Oracle DBA | SQL Server, Goldengate, Exadata, Big Data, Data ScienceTutorial